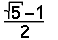Wie errechnet sich der Goldene Schnitt ?

Gegeben sei eine Strecke s, die in zwei Teilstrecken k und g aufgeteilt ist.
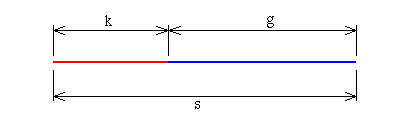
Laengenverhaeltnisse des Goldenen Schnitts
Allgemein gilt: 
 s = k + g         (Gleichung I)

Im Falle des Goldenen Schnitts gilt ausserdem: 

 k    g
 - =  -            (Gleichung II)
 g    s
Also, das Verhältnis der kleinen Strecke k zur großen g verhält sich wie die große Strecke g zur Gesamtstrecke s.

Man setzt nun Gleichung I in Gleichung II ein 

 k    g
 - =  -            (Gleichung III)
 g   k+g

und löst nach k auf. Nach einigen Umformungen erhält man schließlich: 

 k = Die Goldene Zahl * g
 

 k = 0.6180339887... * g

D.h., der goldene Schnitt stellt sich ein, wenn zwei Strecken im Verhältnis 0.618... zu 1 zueinander stehen. Für Liebhaber von ganzen Zahlen ergeben die Verhältnisse 3 zu 5 gleich 0.6 bzw. 8 zu 13 gleich 0.6154 gute Näherungen. 13 zu 21 gleich 0.619 liegt schon nur noch ein Promill vom exakten Wert entfernt. Leider gibt es keinen ganzzahligen Bruch mit dem sich der goldene Schnitt exakt bestimmen ließe. Er ist also eine irrationale Zahl. Weiter unten werden wir aber sehen, dass wir uns der Zahl mittels eines Kettenbruches beliebig genau nähern können.

Die Zahl 0.6180339887... wird häufig als φ (phi) oder "Major des Goldenen Schnittes" bezeichnet.
Der Minor des Goldenen Schnittes" berechnet sich zu: 

 1 - φ = 0.3819660112...

 

 

Als kleine mathematische Spielerei kann man nun den Kehrwert von 0.6180339887... bilden und erhält 

       1
 ---------------   = 1.6180339887...
 0.6180339887...
( Diese Zahl wird häufig als Φ (Phi) bezeichnet. )
Auffällig ist, daß die Nachkommastellen absolut identisch sind, d.h., 0.6180339887... ist die Lösung zu der Gleichung 
 1
 - =  1 + φ        (Gleichung IV)
 φ
Bei genauerem Hinsehen erkennt man, daß Gleichung IV ein Sonderfall von Gleichung III ist, der sich für g = 1 einstellt.


Mit:

Φ = 1 + φ    (Gleichung V)

und

    1
Φ = -        nach φ umgeformt:
    φ

    1
φ = -        (Gleichung VI)
    Φ

ergibt sich:
        1
Φ = 1 + -    (Gleichung VII)
        Φ


Setzt man Gleichung VII wiederholt in sich selbst ein, gelangt man schließlich zu einem unendlichen Kettenbruch:

         1           1                            1
Φ =  1 + -  =  1 + -----  =  ...  =  1 + -------------------
         Φ             1                            1
                   1 + -                 1 + ---------------
                       Φ                              1
                                             1 + -----------
                                                        1
                                                 1 + -------
                                                           1
                                                     ... + -
                                                           Φ

Damit läßt sich sehr effizient ein Programm (hier in C) zur Berechnung von Φ erstellen.

 

 

Ein erstaunliches Phänomen:
Bildet man ein rechtwinkliges Dreieck mit den Katheten a = φ = 0.6180339887... und b = 1, so ergibt sich die Hypotenuse c zu: 

 c2 = a2 + b2

 c2 = 0.61803398872 + 12

 c2 = 0.3819660112 + 1

 c = 1.175570504...
Konstruiert man in einen Einheitskreis mit r=1 ein gleichseitiges Fünfeck, so ergibt sich die Länge einer Seite s5 ebenfalls zu 1.175570504, und zwar nicht ungefähr, sondern ganz genau! Kann mir das jemand erklären ????
 

 
 

Linksammlung zum Goldenen Schnitt:
Die Triangulation des Rechtecks

Sie kennen noch weitere interessante Seiten zum Goldenen Schnitt? Dann schicken Sie mir doch netter Weise den Link per Email.

 

E N D E
27.08.1998   Rainer Hofmann
Zuletzt geändert am: 07.11.2019